Problem 1

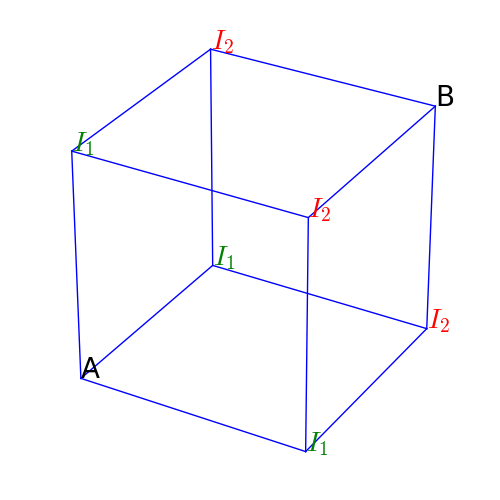
There is an ant sitting on the lower left vertex of a cube (vertex A), at each step the ant randomly moves to an adjecent vertex with equal probability. What is the expected number of steps it would take ant to reach the upper right vertex of this cube (vertex B)?

Solution

The expected distance in terms of steps from A to B depends on the expected distance between the adjecent vertexes of A and B. The adjacent vertexes of A are all labelled as \(I_1\) because, by symmetry, the expected distances from them to B are identical. In turn, the expected distance from \(I_1\) to B depends on the expected distance from the adjacent vertexes of \(I_1\) to B. In this case, \(I_1\) has two kinds of adjacent vertexes: A and those labelled as \(I_2\). Moreover, from an vertex \(I_1\), the ant has probability 1/3 of going back to A and probability 2/3 of going to \(I_2\).

Continuing this argument on \(I_2\), we would reach a recursive (and circular) relations among the distnaces from A, from \(I_1\) and from \(I_2\) to B.

Before we wirte down the equtions, we introduce some notations:

$$\begin{align} R_0 : \text{ distance } A \rightarrow B \\ R_1 : \text{ distance } I_1 \rightarrow B \\ R_2 : \text{ distance } I_2 \rightarrow B. \end{align}$$

Now, we give the recursive equations for R_0, R_1 and R_2:

$$\begin{align} & \left\{ \begin{array} [c]{l} R_0 = 1 + R_2 \\ R_1 = 1 + \frac{1}{3} R_0 + \frac{2}{3} R_2 \\ R_2 = 1 + \frac{2}{3} R_1 \end{array} \right. \\ \Rightarrow & \left\{ \begin{array} [c]{l} R_0 = 10 \\ R_1 = 9 \\ R_2 = 7 \end{array} \right. \end{align}$$

So, on average it takes the ant 10 steps from A to B.

Problem 2

What is the expected number of tosses it would take to see all six faces of a dice?

Source

Method I: Recursive Expectation

It’s a little hard to set up this problem, but once your practice more this kind of problem, you will get used to it. Let’s denote \(E_i, i=1,\cdots,6\) to be the expected number of tosses to see all faces, given that there are \(i\) remaining faces to be seen. In other words, if you’ve already seen \(6-i\) faces, it would still take on average \(E_i\) number of tosses to see all faces. In this case, \(E_6\) is what we are looking for.

Now, we can write down the recursive equations:

$$\begin{equation} \left\{ \begin{array} [c]{l} E_1 = \frac{1}{6} + \frac{1}{6}\left(1+E_1\right) \Rightarrow E_1 = 6,\\ E_2 = \frac{2}{6}\left(1+E_1\right) + \frac{4}{6}\left(1+E_2\right) \Rightarrow E_2 = 9,\\ E_3 = \frac{3}{6}\left(1+E_2\right) + \frac{3}{6}\left(1+E_3\right) \Rightarrow E_3 = 11,\\ E_4 = \frac{4}{6}\left(1+E_3\right) + \frac{2}{6}\left(1+E_4\right) \Rightarrow E_4 = \frac{25}{2},\\ E_5 = \frac{5}{6}\left(1+E_4\right) + \frac{1}{6}\left(1+E_5\right) \Rightarrow E_5 = \frac{137}{10},\\ E_6 = 1 + E_5 \Rightarrow E_6 = \frac{147}{10}. \end{array} \right. \end{equation}$$

As seen in my last post, a state transition diagram might help understanding the above equations:

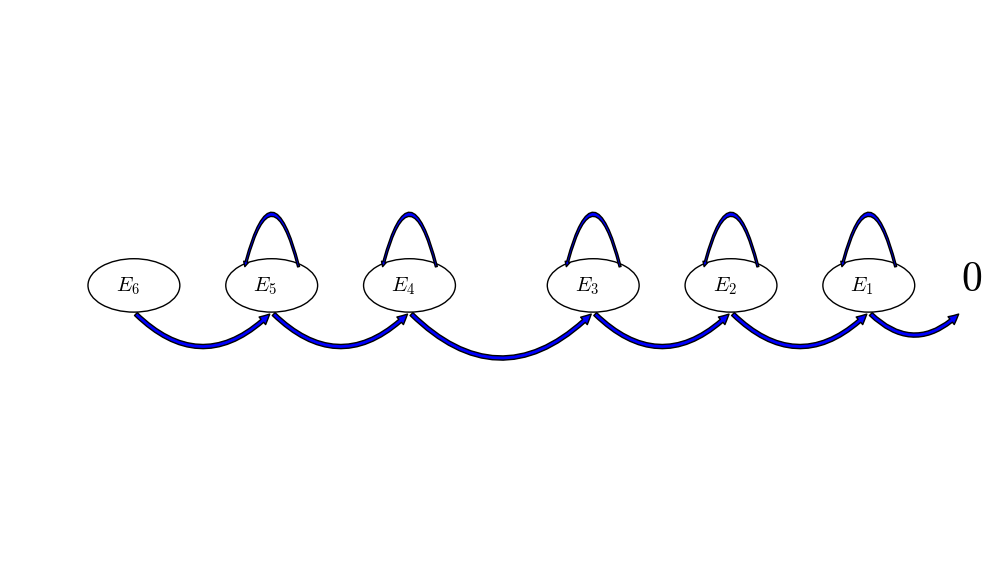
We can see from above that this system of equations can be solved sequentially, and in the end we know that it takes on average 14.7 number of tosses to see all six faces of a dice.

Method II: Geometric Distribution

This method of solving this problem might seem more straightforward. I put it in the second place, because I would like to emphasize recursive expectation in this post and last post as well. Also, geometric distribution is a particular probaiblity distributtion that is not as widely applicable as the technique of recursive expectation.

The argument goes like this: it takes, of course, (on average) 1 toss to see one face; after seening one, the number of tosses it takes to see a second new faces is a geometric distribution with parameter 5/6, hence the expectation is 6/5; then after seeing two faces, the number of tosses it takes to see a third new face is a geometric distribution with parameter 4/6=2/3, hence the expectation is 3/2; …

We’ve seen that the expected number of tosses it takes between seeing the \(i\)th face and the \(i+1\)th face is \(6/(6-i),i=0,\cdots,5\), therefore the expected number of tosses it takes to see all six faces is

$$\begin{equation} \sum_{i=0}^5 \frac{6}{6-i} = \frac{147}{10}. \end{equation}$$

We’ve arrived at the same conclusion that it takes on average 14.7 tosses to see all six faces of a dice.