Method I: Polar Coordinates

How to randomly and uniformly smaple k items out of a population (of an unknow size)?

Problem 1

Source

Problem

Suppose we toss a fair coin, what is the expected number of tosses until we get two heads in a row?

I’ll show three ways of solving this problem.

Method I: Recursive Expectation in Two Steps

Let \(X\) be the number of tosses until we get two heads in a row, then we use the recursive relations of expectations to write down an equation of \( \mathbb{E}\left[X\right] \) as follows:

$$\begin{align} & \mathbb{E}\left[X\right] = \frac{1}{2}\cdot \mathbb{E}\left[X\vert T\right]+\frac{1}{4}\cdot \mathbb{E}\left[X\vert HT\right]+\frac{1}{4}\cdot \mathbb{E}\left[X\vert HH\right] \\ \Rightarrow & \mathbb{E}\left[X\right] = \frac{1}{2}\cdot \left(1+\mathbb{E}\left[X\right]\right)+\frac{1}{4}\cdot \left(2+\mathbb{E}\left[X\right]\right)+\frac{1}{4}\cdot 2 \\ \Rightarrow & \mathbb{E}\left[X\right]=6. \end{align}$$

This recursive relation can be better explained by the probabilistic tree below:

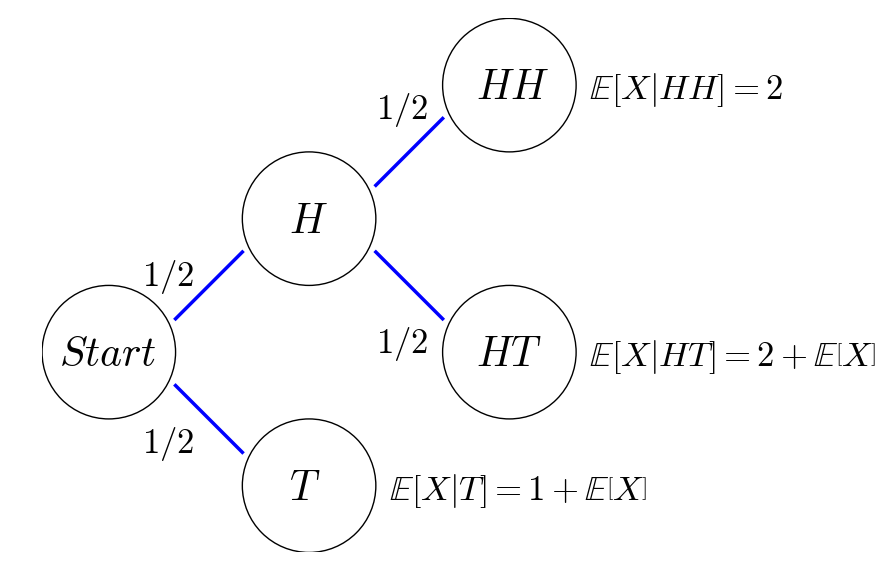
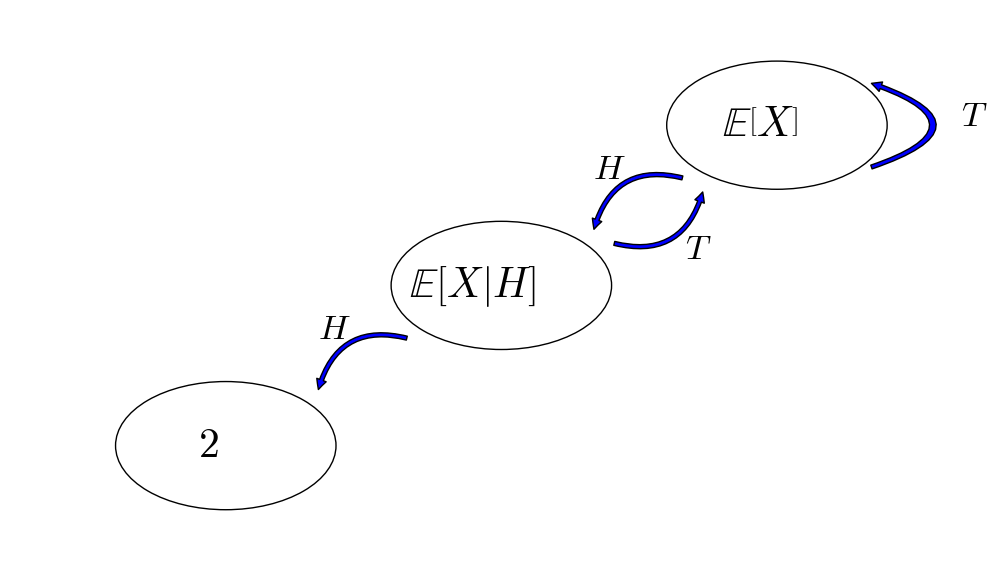
For those who know Markov chains, we can also draw a state transition diagram as follows:

Method II: Recursive Expectation in One Step

This mehod is almost the same as Method I, except that we use the recursive relations of expections to write down a system of equations to solve:

$$\begin{align} & \left\{ \begin{array} [c]{l} \mathbb{E}\left[X\right] = \frac{1}{2} \cdot \mathbb{E}\left[X\vert H\right] + \frac{1}{2}\cdot \left(1+\mathbb{E}\left[X\right]\right) \\ \mathbb{E}\left[X\vert H\right] = \frac{1}{2}\cdot 2 + \frac{1}{2}\cdot \left(2+\mathbb{E}\left[X\right]\right) \end{array} \right. \\ \Rightarrow & \left\{ \begin{array} [c]{l} \mathbb{E}\left[X\right] = 6 \\ \mathbb{E}\left[X\vert H\right] = 4 \end{array} \right. \end{align}$$

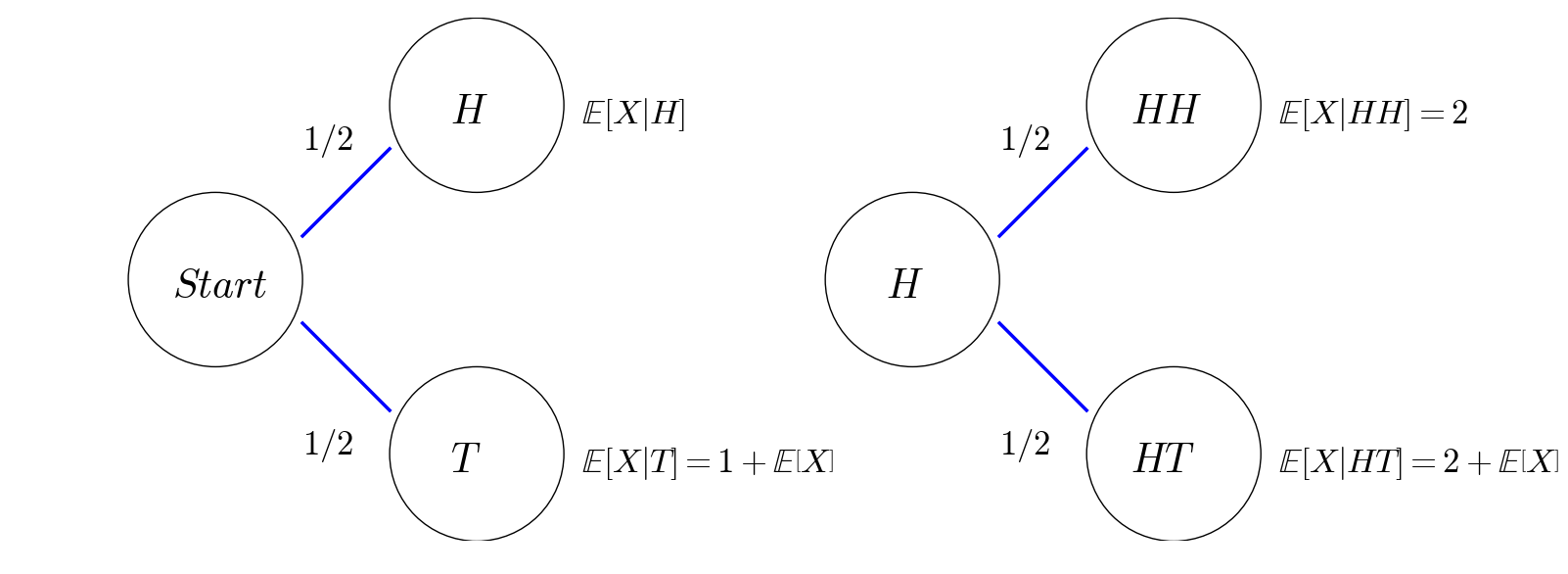
As you see more examples in my next post, it is more common to formulate a system of equation, rather than a single equation, for the problem of recursive expectations.

Method III: Martingale Approach (Optional)

We introduce a random process \( X_n,n\geq 1 \) as a random process to represent the coin toss process, that is,

$$\begin{equation} X_n = \left\{ \begin{array}{cl} 1, & \text{if the nth coin toss is head}, \\ -1, & \text{if the nth coin toss is tail}. \end{array} \right. \end{equation}$$

Note that \( X_n \) is a martingale. And we use another random process \( Y_n,n\geq 1 \) to represent our trading strategy,

$$\begin{align} Y_1 & = 1, \\ Y_n & = 2\cdot 1_{\{X_{n-1}=1\}} + 1_{\{X_{n-1}=-1\}}, n\geq 2. \end{align}$$

This means that we start our first bet with \($1\), then we double our bet to \($2\) if the previous coit toss turns out to be head and still bet \($1\) otherwise.

Consequently, our wealth process \(Z_n = Y_1X_1 + \sum_{i=2}^n Y_i(X_i - X_{i-1})\) is given by

$$\begin{align} Z_1 & = 2\cdot 1_{\{X_1=1\}} - 1, \\ Z_n & = \sum_{i=2}^n 4\cdot 1_{\{X_i=1,X_{i-1}=1\}} + 2\cdot 1_{\{X_n=1\}} - n, n\geq 2. \end{align}$$

Indeed, \(Z_n\) is a discrete-time stochastic integral with respect to \(X_n\), and therefore, \(Z_n\) is also a martingale.

Now, we define a stopping time \(\tau = \min\{n\geq 2: X_n = 1, X_{n-1}=1\}\). The definition of \(\tau\) would imply that \(X_1=\cdots=X_{\tau-2}=0,X_{\tau-1}=X_{\tau}=1\).

Finally, we invoke the optinal sampling theorem to get

$$\begin{align} 0 = \mathbb{E}\left[Z_{\tau}\right] & = 4\cdot 1_{\{X_{\tau}=1,X_{\tau-1}=1\}}+2\cdot 1_{\{X_{\tau}=1\}} - \mathbb{E}\left[\tau\right] \\ & = 4 + 2 - \mathbb{E}\left[\tau\right] \\ & \Rightarrow \mathbb{E}\left[\tau\right] = 6. \end{align}$$

In this post, I will share some resources and practical tips about how to get a quant job.

Preparation

Source

Generally, a quant needs to know:

• Programming
• Math
• Stats (Machine Learning)
• Finance

Note: math used to be importmant when derivative pricing was just becoming popular, however, nowdays I feel that the demand for quants who build mathematical models decreases dramatically. On the other hand, quants need to code more. Thus, I put programming in the first place.

An example of a quant job description is this.

Apparently, it is hard to be an expert in all four areas. Ideally, a candidate is strong in one area, while knowing a little bit about other areas.

For those STEM majors, it is worthwhile spending some time learning about finance. A good choice is to study the CFA Program. If you can pass at least its Level I Exam, you should already have a basic yet comprehensive knowledge of finance.

Now, statistics plus computer science become a new buzzword: machine learning. If you want to get your foot into the door, consider taking a MOOC course like Andrew Ng’s Machine Learning. To get some hands-on experience of machine learning, take a look at Kaggle, an excellent data science competition platform.

Application

Most firms in the quant space accept online applications, a great place to start is this quant firm list.

Source

Apply early. Big investment banks typically have their own recruiting cycles, so don’t miss their deadlines.

Resume

Learn from good examples: Princeton MFin students’ resume book.

Cover Letter

Not many firms ask for a cover letter. My cover letter simply expands my resume, and elaborates on my past experience on math, stats (machine learning), programming and finance.

Interview

Interview questions can be quite comprehensive, covering math, stats (machine learning), programming and finance.

Classic quant interview books include:

• Heard on the Street: Quantitative Questions from Wall Street Job Interviews
• A Practical Guide To Quantitative Finance Interviews

Before an interview, I would also check:

• Glassdoor
• Interviewer’s LinkedIn profile

In this blog, I will constantly post some most commonly asked interview questions.

It usually take several rounds of phone interviews and one on-site interview to get an offer.

The more interviews your get, the stronger your become as a candidate. Persistence is key! I hope this blog post is useful to those who are interested in quant jobs.

//////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////

我在本文中将分享一些资源和个人经验，希望能帮助那些对金融宽客（一下简称宽客）感兴趣的人找到工作。

准备

图片来源

总体来说，一个宽客需要了解的知识包括:

• 编程
• 数学
• 统计（机器学习）
• 金融

注：数学在早些年衍生品刚刚流行的时候比较重要，但现在我觉得那些单纯做数学建模的宽客越来越少了，而现在越来越多的宽客需要写程序，所以我就把编程放在了第一位。

这里是一个典型的宽客职位描述。

显然，一个人很难在以上四个方面都成为专家。求职者最好能在一个方面有所专长，而其他方面也能略知一二。

对于理工科（STEM）专业的学生来说，或许值得花些时间学习一些金融知识。参加特许金融分析师项目是一个不错的选择。如果你能至少考过特许金融分析师一级考试，那么你应该就已经对金融有了一个基本但全面的了解。

如今，统计加上计算机变成了一个热门的新名词：机器学习。如果你想学习一点机器学习的基本知识，那么可以考虑去上一些网络课程比如吴恩达教授的机器学习课程。如果你也想增加一些机器学习的动手经验，可以去看看一个非常优秀的数据科学竞技平台Kaggle。

申请

大多数招宽客的公司都接受网上申请，这里是一个很好的各公司网申地址的清单。

图片来源

趁早申请。大的投行通常都有各自的招聘季，所以别错过它们的神情截止日期。

简历

从好的简历样本中学习：普林斯顿大学金融硕士项目学生简历簿。

求职信

不会有太多公司要求有求职信。我的求职信其实就是简历的扩展，也就是具体描述了我在编程、数学、统计（机器学习）和金融这些领域的经验。

面试

面试问题涉及面可以很广，包括编程、数学、统计（机器学习）和金融。

经典的宽客面试书有：

• Heard on the Street: Quantitative Questions from Wall Street Job Interviews
• A Practical Guide To Quantitative Finance Interviews

面试前，我通常也会去看：

• Glassdoor
• 面试官的LinkedIn页面

在我的博客中，我也会陆续分享一些经常被问到的面试题。

面试过程通常包括好几轮电话面试和最终的造访公司面试。

你面得越多，就会越强。坚持到底就是胜利！希望本文对那些对宽客工作感兴趣的人有所帮助。