How to generate random points uniformly on a circle of radius R?
Method I: Polar Coordinates
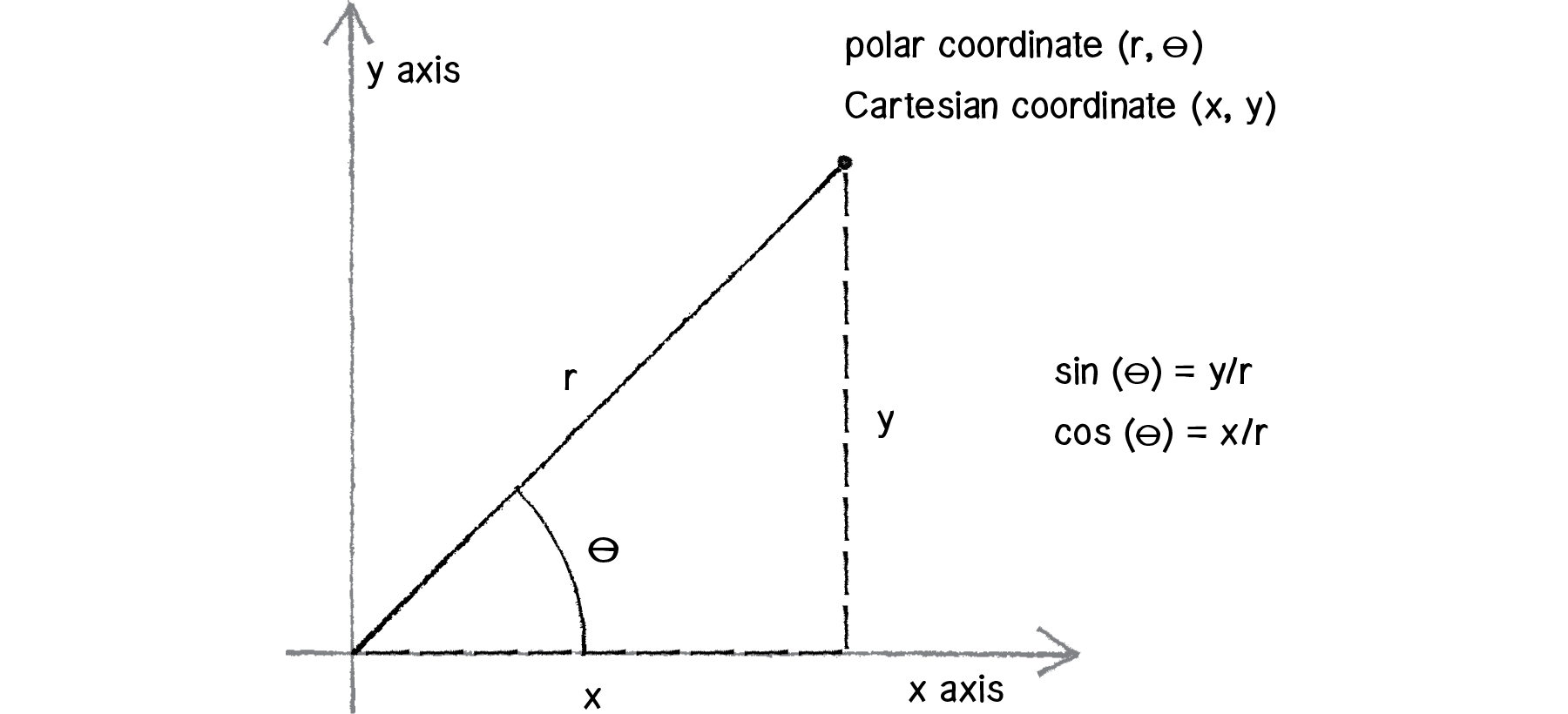
A naive first thought: Oh, we might just generate a uniform random radius \(r\in [0,R]\) and a uniform random angle \(\theta\in [0,2\pi]\), and we are basically done?
However, if we simulate using this naive method, we will see that points clustered around the center of the circle, as shown in the left picture below:
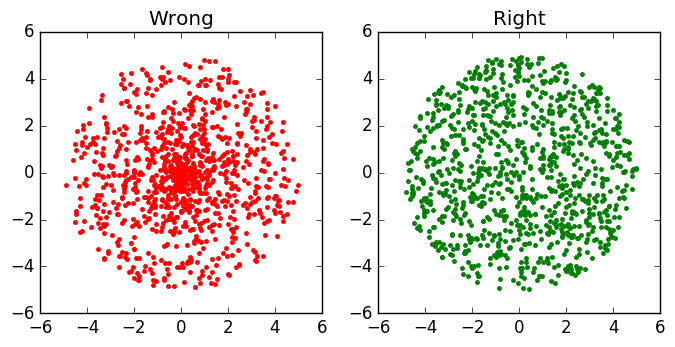
Something must be wrong.
Key intuition: for a certain angle interval \([\theta, \theta+d\theta]\), there needs to be more points generated further out (at large \(r\)) than close to zero.
Recall that, in polar coordinates, the infinitesimal area is \(rdrd\theta\).
Then, the pdf of \(r\) should be proportional to \(r\). Actually, it is \(f(r)=\frac{2}{R^2}r\) due to normailization.
Now, we can use the inverse cdf to generate \(r\):
where \(\text{rand()}\) is a uniformly distributed random number in \([0,1]\).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
import numpy as np
import matplotlib.pyplot as plt
plt.close("all")
# setup
Nmax = 1000
R = 5
# wrong method
r1 = R * np.random.rand(Nmax, 1)
theta1 = 2 * np.pi * np.random.rand(Nmax, 1)
x1 = r1 * np.cos(theta1)
y1 = r1 * np.sin(theta1)
# right method
# pdf_r(r)=(2/R^2) * r
# cumulative pdf_r is F_r = (2/R^2)* (r^2)/2
# inverse cumulative pdf is r = R*sqrt(F_r)
r2 = R * np.sqrt(np.random.rand(Nmax, 1))
theta2 = 2 * np.pi * np.random.rand(Nmax, 1)
x2 = r2 * np.cos(theta2)
y2 = r2 * np.sin(theta2)
# plot
plt.subplot(121)
plt.plot(x1,y1,'r.')
plt.xlim((-1.1*R,1.1*R))
plt.ylim((-1.1*R,1.1*R))
plt.title('Wrong')
plt.axis('square')
plt.subplot(122)
plt.plot(x2,y2,'g.')
plt.xlim((-1.1*R,1.1*R))
plt.ylim((-1.1*R,1.1*R))
plt.title('Right')
plt.axis('square')
plt.show()
plt.savefig("random_point_on_circle", bbox_inches='tight')
Method II: Limit Of Shrinking Triangles (Optional)
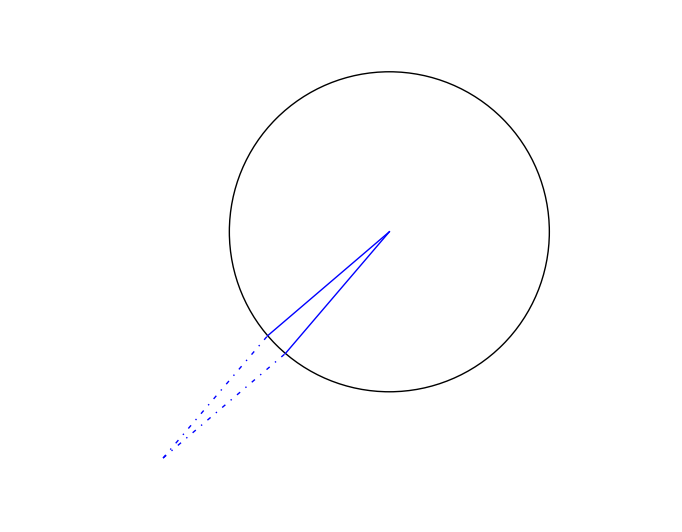
Think of the circle consisting of an infinite amount of infinitesimal sectors, which is shown below in solid lines. To generate uniform random points in such a sector, we can first generate random points in the parallelogram containing the sector, then fold back those points that fall into the outside triangle as shown below in dotted lines.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# setup
Nmax = 1000
R = 5
# simulating limiting triangles
theta2 = 2 * np.pi * np.random.rand(Nmax, 1)
r2 = R * np.random.rand(Nmax, 1) + R * np.random.rand(Nmax, 1)
r2[r2>R] = 2*R - r2[r2>R] # if r2>R then r2 = 2*R - r2 else r2 = r2
x2 = r2 * np.cos(theta2)
y2 = r2 * np.sin(theta2)
# plot
plt.figure()
plt.plot(x2,y2,'g.')
plt.xlim((-1.1*R,1.1*R))
plt.ylim((-1.1*R,1.1*R))
plt.title('Right')
plt.axis('square')
plt.show()