Source

Problem

Suppose we toss a fair coin, what is the expected number of tosses until we get two heads in a row?

I’ll show three ways of solving this problem.

Method I: Recursive Expectation in Two Steps

Let \(X\) be the number of tosses until we get two heads in a row, then we use the recursive relations of expectations to write down an equation of \( \mathbb{E}\left[X\right] \) as follows:

$$\begin{align} & \mathbb{E}\left[X\right] = \frac{1}{2}\cdot \mathbb{E}\left[X\vert T\right]+\frac{1}{4}\cdot \mathbb{E}\left[X\vert HT\right]+\frac{1}{4}\cdot \mathbb{E}\left[X\vert HH\right] \\ \Rightarrow & \mathbb{E}\left[X\right] = \frac{1}{2}\cdot \left(1+\mathbb{E}\left[X\right]\right)+\frac{1}{4}\cdot \left(2+\mathbb{E}\left[X\right]\right)+\frac{1}{4}\cdot 2 \\ \Rightarrow & \mathbb{E}\left[X\right]=6. \end{align}$$

This recursive relation can be better explained by the probabilistic tree below:

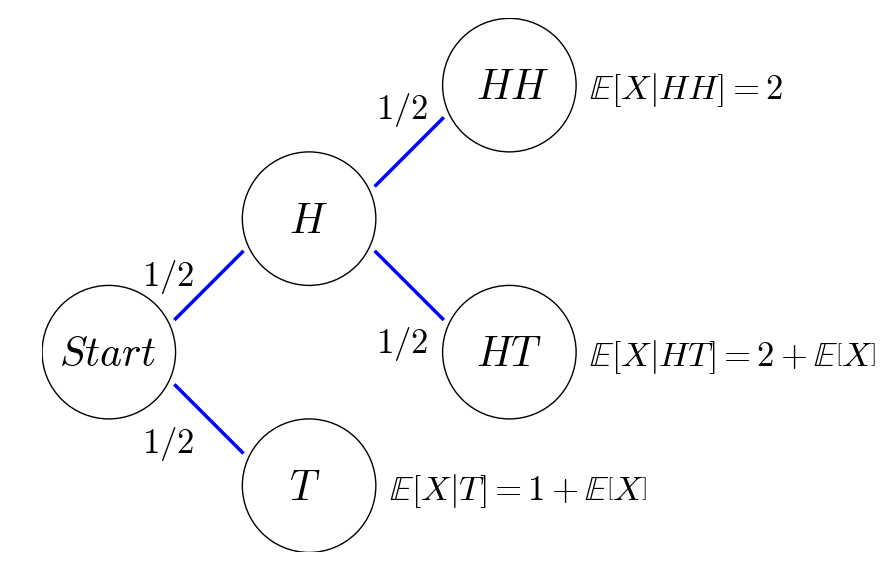
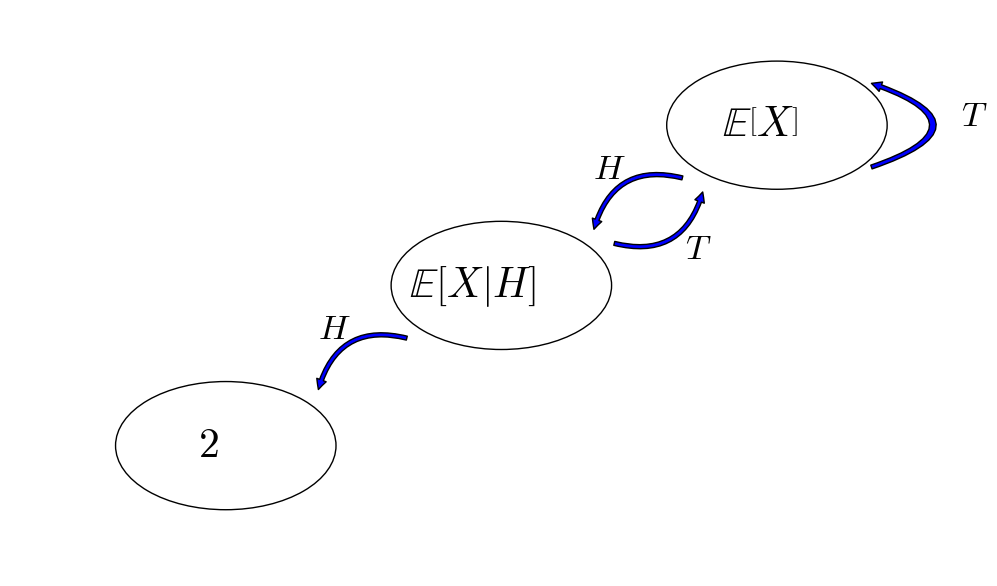
For those who know Markov chains, we can also draw a state transition diagram as follows:

Method II: Recursive Expectation in One Step

This mehod is almost the same as Method I, except that we use the recursive relations of expections to write down a system of equations to solve:

$$\begin{align} & \left\{ \begin{array} [c]{l} \mathbb{E}\left[X\right] = \frac{1}{2} \cdot \mathbb{E}\left[X\vert H\right] + \frac{1}{2}\cdot \left(1+\mathbb{E}\left[X\right]\right) \\ \mathbb{E}\left[X\vert H\right] = \frac{1}{2}\cdot 2 + \frac{1}{2}\cdot \left(2+\mathbb{E}\left[X\right]\right) \end{array} \right. \\ \Rightarrow & \left\{ \begin{array} [c]{l} \mathbb{E}\left[X\right] = 6 \\ \mathbb{E}\left[X\vert H\right] = 4 \end{array} \right. \end{align}$$

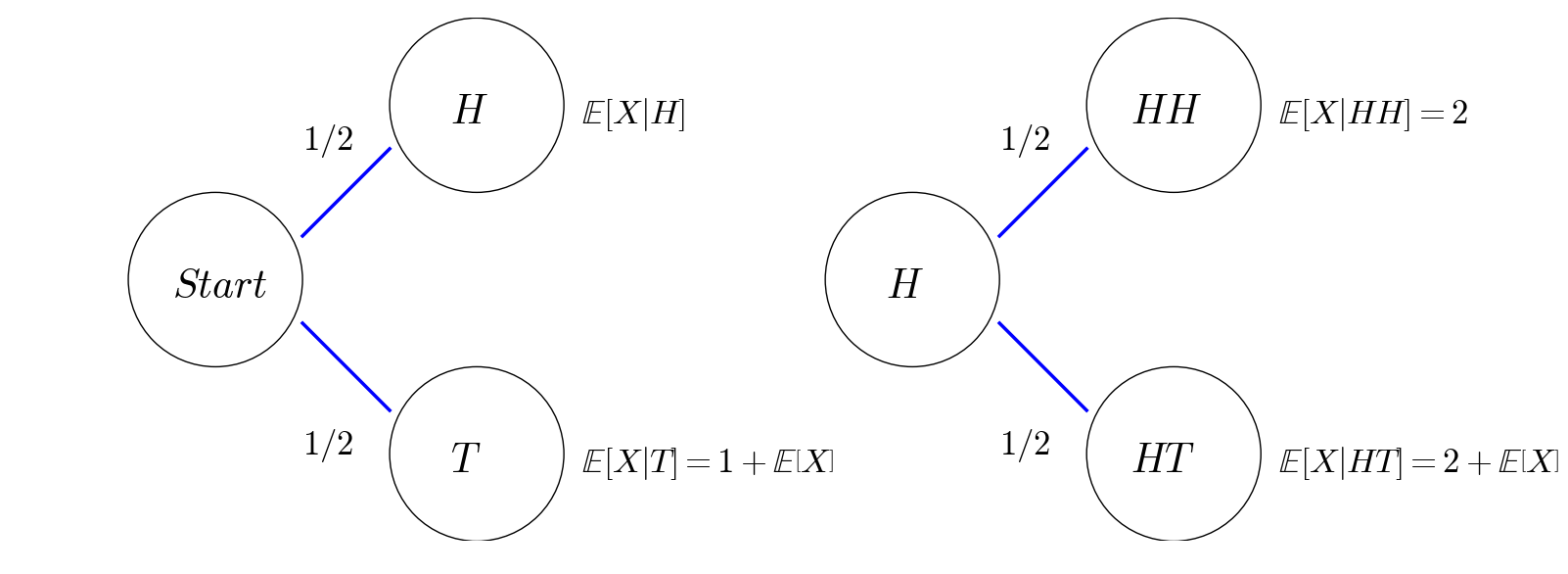
As you see more examples in my next post, it is more common to formulate a system of equation, rather than a single equation, for the problem of recursive expectations.

Method III: Martingale Approach (Optional)

We introduce a random process \( X_n,n\geq 1 \) as a random process to represent the coin toss process, that is,

$$\begin{equation} X_n = \left\{ \begin{array}{cl} 1, & \text{if the nth coin toss is head}, \\ -1, & \text{if the nth coin toss is tail}. \end{array} \right. \end{equation}$$

Note that \( X_n \) is a martingale. And we use another random process \( Y_n,n\geq 1 \) to represent our trading strategy,

$$\begin{align} Y_1 & = 1, \\ Y_n & = 2\cdot 1_{\{X_{n-1}=1\}} + 1_{\{X_{n-1}=-1\}}, n\geq 2. \end{align}$$

This means that we start our first bet with \($1\), then we double our bet to \($2\) if the previous coit toss turns out to be head and still bet \($1\) otherwise.

Consequently, our wealth process \(Z_n = Y_1X_1 + \sum_{i=2}^n Y_i(X_i - X_{i-1})\) is given by

$$\begin{align} Z_1 & = 2\cdot 1_{\{X_1=1\}} - 1, \\ Z_n & = \sum_{i=2}^n 4\cdot 1_{\{X_i=1,X_{i-1}=1\}} + 2\cdot 1_{\{X_n=1\}} - n, n\geq 2. \end{align}$$

Indeed, \(Z_n\) is a discrete-time stochastic integral with respect to \(X_n\), and therefore, \(Z_n\) is also a martingale.

Now, we define a stopping time \(\tau = \min\{n\geq 2: X_n = 1, X_{n-1}=1\}\). The definition of \(\tau\) would imply that \(X_1=\cdots=X_{\tau-2}=0,X_{\tau-1}=X_{\tau}=1\).

Finally, we invoke the optinal sampling theorem to get

$$\begin{align} 0 = \mathbb{E}\left[Z_{\tau}\right] & = 4\cdot 1_{\{X_{\tau}=1,X_{\tau-1}=1\}}+2\cdot 1_{\{X_{\tau}=1\}} - \mathbb{E}\left[\tau\right] \\ & = 4 + 2 - \mathbb{E}\left[\tau\right] \\ & \Rightarrow \mathbb{E}\left[\tau\right] = 6. \end{align}$$